Using freemat is able to help us to solve systems of equations with imaginary solutions.
Here is the assignment that we need to do
1.
Compute by hand
Compute by freemat
2.
3.
4.
Saturday, May 26, 2012
Freemat with complex number
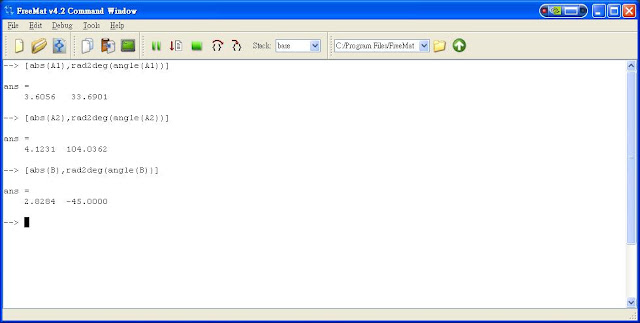
Since we introduced new elements such as capacitors and inductors. They contain imaginary part of the resistance. Thus, we will need to deal the imaginary number i or j in the equations a lot
Using freemat is able to help us to solve systems of equations with imaginary solutions.
Here is the assignment that we need to do
1.
Compute by hand
Compute by freemat
2.
3.
4.
Using freemat is able to help us to solve systems of equations with imaginary solutions.
Here is the assignment that we need to do
1.
Compute by hand
Compute by freemat
2.
3.
4.
Impedance and AC Analysis I
In this experiment, we will introduce how "real" inductor, which is model as a series resistance to account for the resistance of the wires inside the inductor
Th impedance looking into a real inductor will be
Z=R_L+jwL
and the magnitude of the impedance is the magnitude of Z
|Z|=sqrt(R_L^2+(wL)^)
first, we measured the internal resistance of the inductor
R_L=3.4ohm
next we want to apply a known AC voltage and measure the resultant AC current
Here R_ext is used to limit the current. The function generator has an internal resistance of about 50ohm. Also, we assume the ammeter has no voltage drop
We will use R_ext =68.5ohm
Next we will set the RMS voltage of the function generator with 20KHZ
Secondly, we will device the circuit and record the reading from the multimeter and ammeter
V_in=4.53V
I_in=88mA
The reading is different from the FB display because there is some internal resistance due to the function generator.
Calculations:
Z=V/I = 4.52/88mA=51.36ohm
Z=R_ext+R_L+jwL
|Z|=sqrt((R_ext+R_L)^2+(wL)^2))
W=2pif=2pi*20000=125664rad/s
Since we know the value of Z, R_ext, R_L and w
we will need to find L, which is about 0.4mH
Next we will consider the circuit that will add a capacitor that is in series with the inductor to try to cancel the inductive par of the real inductor impedance
to know what is the value of capacitor
we set
wL=1/wC
C=1.58*10-7 F
since there is no capacitor box to use
we find the closest value of capacitor to use in the circuit, which is 1.51*10^-7F
Thus, we need to go back and redo the math to find the critical frequency
f = 1/(2*pi*50.27*.151*10^-6)=20.97KHz
Next, we take scope to measurements at 20.97KHZ
V_PP_CH1=23.08V
V_PP_CH2=19.49
delta_t=19.46 us
phase angle = w*t*180/pi=125664*19.46*10^-6*180/pi=146 degree
Next, we used DDM to measure the voltage and current at different frequency
Follow-up question
1. Why is the input current that largest at 12.7K?
The input current is largest because the impedance of the element is the smallest
2. Calculate the theoretical voltage phasor across the real inductor at 20.97KHz (use the DMM measurement value as the source voltage phasor magnitude). Compare this with the scope measurements. Convert the scope measurement to RMS for comparison purposes.
(23.08/(2sqrt(2))*2pi*20.97*1000*0.4*10^-3/(68.5+3.4)=5.98V
19.49/(2sqrt(2))=6.89
(6.89-5.98)/5.98=15.2%
3. Does the circuit look more capacitive or inductive at frequencies below 20kHZ?
capacitive
4. Does the circuit look more capacitive or inductive at frequencies above 20kHZ?
inductive
Z=R_L+jwL
and the magnitude of the impedance is the magnitude of Z
|Z|=sqrt(R_L^2+(wL)^)
first, we measured the internal resistance of the inductor
R_L=3.4ohm
next we want to apply a known AC voltage and measure the resultant AC current
We will use R_ext =68.5ohm
Next we will set the RMS voltage of the function generator with 20KHZ
Secondly, we will device the circuit and record the reading from the multimeter and ammeter
V_in=4.53V
I_in=88mA
The reading is different from the FB display because there is some internal resistance due to the function generator.
Calculations:
Z=V/I = 4.52/88mA=51.36ohm
Z=R_ext+R_L+jwL
|Z|=sqrt((R_ext+R_L)^2+(wL)^2))
W=2pif=2pi*20000=125664rad/s
Since we know the value of Z, R_ext, R_L and w
we will need to find L, which is about 0.4mH
Next we will consider the circuit that will add a capacitor that is in series with the inductor to try to cancel the inductive par of the real inductor impedance
to know what is the value of capacitor
we set
wL=1/wC
C=1.58*10-7 F
since there is no capacitor box to use
we find the closest value of capacitor to use in the circuit, which is 1.51*10^-7F
Thus, we need to go back and redo the math to find the critical frequency
f = 1/(2*pi*50.27*.151*10^-6)=20.97KHz
Next, we take scope to measurements at 20.97KHZ
V_PP_CH1=23.08V
V_PP_CH2=19.49
delta_t=19.46 us
phase angle = w*t*180/pi=125664*19.46*10^-6*180/pi=146 degree
Next, we used DDM to measure the voltage and current at different frequency
| Frequency(KHz) | V_in(V) | I_In(mA) | |Z_in|(ohm) |
| 5 | 6.21 | 29.57 | 210 |
| 10 | 6.23 | 48.33 | 108 |
| 20.97 | 5.02 | 69.15 | 72.6 |
| 30 | 5.56 | 66.99 | 83 |
| 50 | 5.96 | 46.93 | 127 |
Follow-up question
1. Why is the input current that largest at 12.7K?
The input current is largest because the impedance of the element is the smallest
2. Calculate the theoretical voltage phasor across the real inductor at 20.97KHz (use the DMM measurement value as the source voltage phasor magnitude). Compare this with the scope measurements. Convert the scope measurement to RMS for comparison purposes.
(23.08/(2sqrt(2))*2pi*20.97*1000*0.4*10^-3/(68.5+3.4)=5.98V
19.49/(2sqrt(2))=6.89
(6.89-5.98)/5.98=15.2%
3. Does the circuit look more capacitive or inductive at frequencies below 20kHZ?
capacitive
4. Does the circuit look more capacitive or inductive at frequencies above 20kHZ?
inductive
AC Signal #1
In this experiment, we will focus on how to measure the phase difference between AC sinusoidal signals at the same frequency. We will see the changes of the capacitor and resistors who are connect in series, while frequency changes.
concepts:
where frequency = 1/period
the phase angle =time difference*w*180/pi
where w = 2pi*f
V_rms=V_pp/(2sqrt(2))
Next, we energize a function generator(FG) and connet to oscilloscope
1.set the FG to produce 10V peak to peak sin wave with 1kHZ
but since we did not use a function generator, we were not able to get 10V peak to peak value but 1V
2.Center the waveform on the scope, adjust the horizontal time-base to display 1 to 2 period on the screen
3. Confirm its 10V peak-to-peak
4. The anticipated RMS value is V_rms=0.371V
when we connet to the DM(digital multimeter) we got a value of V_rms=0.318V
Next, we set the variable resistor box to 1kohm
we calculate the complex impedance of the 100-nF capacitor
Z_cap=(1/wc)=(1/(2pif*100*10^-9))=1591.55ohm
Next, we build the circuit below
Which will look like this
Next, we use the O-scope cursore to find the measure peak-to-peak capacitor voltage on Ch2
V_cap,pp=0.852V
Next, the rms value of the capacitor voltage provided by the DDM
V_cap,rms=0.3012
if we divide 0.852/(2sqrt(2))=0.3012, which is the same value from the reading of multimeter
Next, we measure the time difference between the two waveforms
we get t=105.41 us
where the phase angle will be 37.9 degree
by looking at the graph, CH1 leads CH2
--------------------------------------------------------------------------------
Next, we want to see the affect from changing the frequency
then, we increase the frequency from 1k to 10kHZ
we calculate the new complex impedance of the capacitor
Z_cap=1/wc=159.1ohm
then, we use the o-scope to measure the peak-to-peak capacitor voltage on CH2
V_cap,pp=0.154V
The V_rms value from the multimeter reading is 0.033V
when we divide 0.154/(2sqrt(2))=0.0544, which we can say the values are close
next, we find the time difference, which is 23.78us
the phase angle is 86.61 degree
-----------------------------------------------------------------------------
We return the FG frequency to 1kHZ
increase the resistance box to 10kohm
we do the same thing and find the same value
V_cap,pp=0.178V
V_cap.rms=0.049V
0.178/(2sqrt(2))=0.063V, which are consider close due to the lack of precision due to the equipment
next, the time difference is 221.62 us
where the phase angle is 79.78 degree
Next, we change the value of resistance box untill the capacitor voltage is 2 divisions on the o-scope
we obtain R_box = 3.7K
the V_rms from DDM = 0.119V
time difference=189.19 us
phase angle is 68.1 degree
-------------------------------------------------------------
Finally we set the FG frequency from low to high and observe the impact on the capacitor voltage value
when the frequency is low, the voltage is high
when the frequency is high, the voltage is low
by this observation, we can conclude that the circuit is a lowpass filter
when we adjust the frequency
the higher the frequency, the angle between the resistor and the capacitor is more
Last, we dissemble the circuit and put the parts back to where they belong
With the observations we found in this experiment, we were able to understand that change in frequency and the resistance is able to change the V_rms and the phase angle between the capacitor and resistor. As a result, we were able to control the circuit with desire value of capacitance, resistance and frequency to find a suitable values to do the demand of filter waves
concepts:
where frequency = 1/period
the phase angle =time difference*w*180/pi
where w = 2pi*f
V_rms=V_pp/(2sqrt(2))
Next, we energize a function generator(FG) and connet to oscilloscope
1.set the FG to produce 10V peak to peak sin wave with 1kHZ
but since we did not use a function generator, we were not able to get 10V peak to peak value but 1V
2.Center the waveform on the scope, adjust the horizontal time-base to display 1 to 2 period on the screen
3. Confirm its 10V peak-to-peak
4. The anticipated RMS value is V_rms=0.371V
when we connet to the DM(digital multimeter) we got a value of V_rms=0.318V
Next, we set the variable resistor box to 1kohm
we calculate the complex impedance of the 100-nF capacitor
Z_cap=(1/wc)=(1/(2pif*100*10^-9))=1591.55ohm
Next, we build the circuit below
Which will look like this
Next, we use the O-scope cursore to find the measure peak-to-peak capacitor voltage on Ch2
V_cap,pp=0.852V
Next, the rms value of the capacitor voltage provided by the DDM
V_cap,rms=0.3012
if we divide 0.852/(2sqrt(2))=0.3012, which is the same value from the reading of multimeter
Next, we measure the time difference between the two waveforms
we get t=105.41 us
where the phase angle will be 37.9 degree
by looking at the graph, CH1 leads CH2
--------------------------------------------------------------------------------
Next, we want to see the affect from changing the frequency
then, we increase the frequency from 1k to 10kHZ
we calculate the new complex impedance of the capacitor
Z_cap=1/wc=159.1ohm
then, we use the o-scope to measure the peak-to-peak capacitor voltage on CH2
V_cap,pp=0.154V
The V_rms value from the multimeter reading is 0.033V
when we divide 0.154/(2sqrt(2))=0.0544, which we can say the values are close
next, we find the time difference, which is 23.78us
the phase angle is 86.61 degree
-----------------------------------------------------------------------------
We return the FG frequency to 1kHZ
increase the resistance box to 10kohm
we do the same thing and find the same value
V_cap,pp=0.178V
V_cap.rms=0.049V
0.178/(2sqrt(2))=0.063V, which are consider close due to the lack of precision due to the equipment
next, the time difference is 221.62 us
where the phase angle is 79.78 degree
Next, we change the value of resistance box untill the capacitor voltage is 2 divisions on the o-scope
we obtain R_box = 3.7K
the V_rms from DDM = 0.119V
time difference=189.19 us
phase angle is 68.1 degree
-------------------------------------------------------------
Finally we set the FG frequency from low to high and observe the impact on the capacitor voltage value
when the frequency is low, the voltage is high
when the frequency is high, the voltage is low
by this observation, we can conclude that the circuit is a lowpass filter
when we adjust the frequency
the higher the frequency, the angle between the resistor and the capacitor is more
Last, we dissemble the circuit and put the parts back to where they belong
With the observations we found in this experiment, we were able to understand that change in frequency and the resistance is able to change the V_rms and the phase angle between the capacitor and resistor. As a result, we were able to control the circuit with desire value of capacitance, resistance and frequency to find a suitable values to do the demand of filter waves
First-Order OP AMP Circuit(Integrator)
In this experiment, we will use op-amp as an application with an additional capacitor to maki it into a integrator.
With the integrator, we shell see the change of waveforms for 1000Hz of sine,triangle, square waves
Here is the diagram of circuit
If we do analysis of this circuit and treat the op-amp as an idea op-amp. Also by making R_f>>R_i, will make the current through the capacitor equal to the current trough R_i.
using KCL
we obtain
V_in/R1=ic+(-V_out/Rf)
V_in/R1=-C*(dV_out/dt)
V_out=-1/C*int((V_in/R1) dt)+V_C
Next, we assemble the circuit and have a AC power supply run into the circuit and oscilloscope hook up into the computer to see the change in the wave form
Next, we shell see the picture that appear on the computer
1. Sine Wave
The blue wave is the input wave
the result is in red, which is a inverted sine wave
2. Triangle wave
We can easily see the input is a triangle wave
the output wave is trying to make it into a square wave, but with the lack of the equipment, we can also see the top of the wave is trying to make it into flat line
3. Square Wave
The input clearly is in a square shape
The output is look somewhat like triangle shape or spike shape
Question
When we have a DC component present in the circuit, the capacitor will act like an open switch, thus give us infinite resistance. In this case, the out put voltage will always be the saturated voltage due to the op-amp. Even with high frequency, DC offset will add up as time pass by, and eventually end up with saturated voltage. Thus, we need to add a resistor that is parallel to the capacitor to get rit of any charges that will store in the capacitor.
With the integrator, we shell see the change of waveforms for 1000Hz of sine,triangle, square waves
Here is the diagram of circuit
using KCL
we obtain
V_in/R1=ic+(-V_out/Rf)
V_in/R1=-C*(dV_out/dt)
V_out=-1/C*int((V_in/R1) dt)+V_C
Next, we assemble the circuit and have a AC power supply run into the circuit and oscilloscope hook up into the computer to see the change in the wave form
Next, we shell see the picture that appear on the computer
1. Sine Wave
the result is in red, which is a inverted sine wave
2. Triangle wave
the output wave is trying to make it into a square wave, but with the lack of the equipment, we can also see the top of the wave is trying to make it into flat line
3. Square Wave
The output is look somewhat like triangle shape or spike shape
Question
Capacitor Charging/Discharging
We learned that capacitor is the element that store energy in electrical field. We are able to set the time to charge and discharge by using the desire value of resistors
In this experiment, we will consider charging and discharging a capacitor
we will have a circuit that like the one below
In real life, the capacitor will have a 'leak resistance' that is parallel to the capacitor due to the imperfectness of the world.
We will have two circuits. One for charging the capacitor and one for discharging the capacitor
First, we will need to calculate the expressions for the Thevenin voltage and resistance for the circuits
Charging:
V_Th=Vs* R_leak /(R_leak+R_charge)
R_TH=((R_charge+R_Leak)/R_charge*R_leak))^-1
Discharging:
V_th=Vcap*(R_leak/Rdischarge*Rleak)
R_TH=R_leak*R_discharge/(R_leak+R_discharge)
Next, we need to build and the circuit with a power supply of 9V, and it needs to employ a charging interval of about 20s with a energy of 2.5mJ and discharges with the same amount of energy in 2S
The require capacitance will be
0.5*CV^2=2.5*10^-3 with V=9V
we get C= 61.7 uF
charging resistance
4=R_charge*C where C= 61.7uF
R_charge=64.8kohm
peak current
I=V*e^(-t/4) /R_charge
I_peak=0.139mA
P=1.251mW, and the resistance box is able to handle the power
Again, we need to find the R_discharge value
since we know the time requires is 2s
and tau=2/5
2/5 = R_discharge*C
R_discharge=6.47 kohm
for the peak current:
I_max=1.39mA
P_max=1.39mA*9=12.5mW, and the box is able to handle the power
Next, we obtain the desire value of elements
since there is no capacitor has the exact value we want, we combine three 22uF capacitors in parallel to a close value we want, which we measured is 63.6uF
Next, we assemble the elements on a bread board with multimeter and resistor box hooked up to the circuits
We were able to use logger pro to measure the change in voltage on the capacitor by connecting a probe to the capacitor
This is our result of charging capacitor
This is our result of discharging capacitor
The V_source is 9.01V
Charging:
The final voltage is 8.562V=V_source*R_leak/(R_leak+64.8K)
solve for R_leak, we obtain 1.27Mohm
The V_TH seen by the capacitor is V_th=V_source*(R_leak/R_charge*R_leak)=9.01*(1.27M/(64.8k*1.27M)=8.57 which is voltage seen by the capacitor
Discharging:
V_th=V_source*R_leak/(R_leak+R_discharge)=9.01*1.27M/(1.27M+6.47K)
=8.96V
Follow-up Questions
1. Calculate the Thevenin equivalent voltage and resistance values "seen" by the capacitor during charging
V_TH=8.57V
R_TH= (1.27M+64.8K)/(1.27M*64.8K)=61654ohm
2. Calculate the Thevenin equivalent voltage and resistance values "seen" by the capapcitor during discharging
V_TH=8.96V
R_TH=(1.27M+6.47K)/(1.27M*6.47K)=6437ohm
3. At t equal to one time constant, e^(-t/tau)=e^-1=0.3679: So, when t=tau_c during "charging" the voltage should equal 0.6321*(final voltage). Use this to estimate the value of tau_c from your "charging" waveform. Compute the corresponding value o resistance(this value should be close to the value found in question1)
8.562*0.6321=5.41V
5.41=-10.56e^(-0.2293t)+8.533
t=5.313
5.313=R*C
R=86K ohm
Practical Question
Given: 160MJ , 15k V
1. Determine the required equivalent capacitance
.5*C(15000)^2=160*10^6
C=1.42F
2.If we assume that the capacitance will be achieved in the manner shown below, via a series and parallel combination, calculate the required value of individual capacitance C
1.42=(C^2/2C)*4
C=0.71F
In this experiment, we will consider charging and discharging a capacitor
we will have a circuit that like the one below
In real life, the capacitor will have a 'leak resistance' that is parallel to the capacitor due to the imperfectness of the world.
We will have two circuits. One for charging the capacitor and one for discharging the capacitor
First, we will need to calculate the expressions for the Thevenin voltage and resistance for the circuits
Charging:
V_Th=Vs* R_leak /(R_leak+R_charge)
R_TH=((R_charge+R_Leak)/R_charge*R_leak))^-1
Discharging:
V_th=Vcap*(R_leak/Rdischarge*Rleak)
R_TH=R_leak*R_discharge/(R_leak+R_discharge)
Next, we need to build and the circuit with a power supply of 9V, and it needs to employ a charging interval of about 20s with a energy of 2.5mJ and discharges with the same amount of energy in 2S
The require capacitance will be
0.5*CV^2=2.5*10^-3 with V=9V
we get C= 61.7 uF
charging resistance
4=R_charge*C where C= 61.7uF
R_charge=64.8kohm
peak current
I=V*e^(-t/4) /R_charge
I_peak=0.139mA
P=1.251mW, and the resistance box is able to handle the power
Again, we need to find the R_discharge value
since we know the time requires is 2s
and tau=2/5
2/5 = R_discharge*C
R_discharge=6.47 kohm
for the peak current:
I_max=1.39mA
P_max=1.39mA*9=12.5mW, and the box is able to handle the power
Next, we obtain the desire value of elements
since there is no capacitor has the exact value we want, we combine three 22uF capacitors in parallel to a close value we want, which we measured is 63.6uF
Next, we assemble the elements on a bread board with multimeter and resistor box hooked up to the circuits
The V_source is 9.01V
Charging:
The final voltage is 8.562V=V_source*R_leak/(R_leak+64.8K)
solve for R_leak, we obtain 1.27Mohm
The V_TH seen by the capacitor is V_th=V_source*(R_leak/R_charge*R_leak)=9.01*(1.27M/(64.8k*1.27M)=8.57 which is voltage seen by the capacitor
Discharging:
V_th=V_source*R_leak/(R_leak+R_discharge)=9.01*1.27M/(1.27M+6.47K)
=8.96V
Follow-up Questions
1. Calculate the Thevenin equivalent voltage and resistance values "seen" by the capacitor during charging
V_TH=8.57V
R_TH= (1.27M+64.8K)/(1.27M*64.8K)=61654ohm
2. Calculate the Thevenin equivalent voltage and resistance values "seen" by the capapcitor during discharging
V_TH=8.96V
R_TH=(1.27M+6.47K)/(1.27M*6.47K)=6437ohm
3. At t equal to one time constant, e^(-t/tau)=e^-1=0.3679: So, when t=tau_c during "charging" the voltage should equal 0.6321*(final voltage). Use this to estimate the value of tau_c from your "charging" waveform. Compute the corresponding value o resistance(this value should be close to the value found in question1)
8.562*0.6321=5.41V
5.41=-10.56e^(-0.2293t)+8.533
t=5.313
5.313=R*C
R=86K ohm
Practical Question
Given: 160MJ , 15k V
1. Determine the required equivalent capacitance
.5*C(15000)^2=160*10^6
C=1.42F
2.If we assume that the capacitance will be achieved in the manner shown below, via a series and parallel combination, calculate the required value of individual capacitance C
1.42=(C^2/2C)*4
C=0.71F
Op Amp Application
One of the use of op-amps is to used in scaling and level-shifting application
In this experiment, we will use AS35 , which is an electronic temperature sensor that will produce output voltage that is proportional to the temperature around it to a scale factor of 10mV/degree C. The device only operate at 4-20V and an external resistor to provide an appropriate load.
First, we will verify that the AS35 work. By making the circuit on the breadboard we were able to obtain the temperature of the room is around 22.8 degree C (Vc=0.228V)
We want to convert the temeprature in degree Celsius to Fahrenheit by using the equation
T_F=(1.8Tc)+32
which means we want to scaled the voltage with a factor of 1.8 then shift upword with 320mV
by puting the terms into voltage, we obtain
V_f=(1+(R2/R1))Vc-(R2/R1)Vref
where Vref is 320mV
by using the nodal anlysis at the inverting and non-inverting output we obtain two equations
1+R2/R1=1.8
-R2*Vref/R1=320
we can solve the variable R2 and R1 by choosing R1 to be 1Mohm
thus, R2 will be 0.812Mohm
One thing we need to make sure is output current need to be small. That is the reason why we choose big value of resistor
After device the circuit
and we measure the output voltage
which is 0.711V
By assuming the Vc is exact, we can compute the theoretical value of degree Fahrenheit
In this experiment, we will use AS35 , which is an electronic temperature sensor that will produce output voltage that is proportional to the temperature around it to a scale factor of 10mV/degree C. The device only operate at 4-20V and an external resistor to provide an appropriate load.
First, we will verify that the AS35 work. By making the circuit on the breadboard we were able to obtain the temperature of the room is around 22.8 degree C (Vc=0.228V)
We want to convert the temeprature in degree Celsius to Fahrenheit by using the equation
T_F=(1.8Tc)+32
which means we want to scaled the voltage with a factor of 1.8 then shift upword with 320mV
by puting the terms into voltage, we obtain
V_f=(1+(R2/R1))Vc-(R2/R1)Vref
where Vref is 320mV
by using the nodal anlysis at the inverting and non-inverting output we obtain two equations
1+R2/R1=1.8
-R2*Vref/R1=320
we can solve the variable R2 and R1 by choosing R1 to be 1Mohm
thus, R2 will be 0.812Mohm
One thing we need to make sure is output current need to be small. That is the reason why we choose big value of resistor
After device the circuit
and we measure the output voltage
which is 0.711V
By assuming the Vc is exact, we can compute the theoretical value of degree Fahrenheit
Theoretical Value of Tf = (1.8*0.228+0.32)*100=73.04 degree Fahrenheit
% error = (73.04-71.1)/73.04*100% = 2.66%
which is extremely small
Operational Amplifiers I
A lot of time, we will encounter the situation when that a signal (voltage) that is sent by the sensor is too small/big that we cannot just directly send the signal into the micro-controller(processor). Thus, we need a device to condition the signal. The device we use is call operational amplifiers or Op amps.
the packages it uses have eight legs
In this experiment, we assume that we have a sensor which has an output ranges from 0 to 1V with negligible impedance. The specification for the Signal conditioning needs to be 0 to -10v
and must draw no more than 1mA from the sensor and the op-amp supplies should supply no more than 30mW of power each.
here is the schematic of the circuit
first, we need to determine the value of R1
since the max input voltage is 1 and we want it be lower than 1mA
we can determine the value R1 =(1V)/1mA = 1kΩ
next, we need to determine the feedback resistor
since the max output voltage is 10
10V=Rf/1000
Rf=10KΩ
Next we need to determine Rx
since Rx is to be 1/4W resistor and we want to operate at half of its rated power
The worst case voltage across Rx occurs when Ry is set to zero
(1/8)W=(6^2)/Rx
Rx=1152Ω
Determine Ry
Assuming the value of Rx determined above and no loading on the divider
Ry that will yield 1V across it
1=[Ry/(288+Ry)]6
Ry=57.6Ω
The Thevenin equivalent of the divider circuit from the inverting amplifier
Rth=48Ω
and the thevenin resistance is at least a factor of 20 times smaller than the resistance value for Ri
Next, we devise the experiment
we record the values of the components
Next we build the circuit on the breadboard
Next we record the data from the output by looking at the multimeters we set up for the experiments
Power supply current
Iv1=2.32mA
Iv2=1.49mA
P_V1=12.13*2.32mA=28.14mW
P_V=12.06*1.49mA=17.97mW
Both power supply are less than 30 mW.
the packages it uses have eight legs
In this experiment, we assume that we have a sensor which has an output ranges from 0 to 1V with negligible impedance. The specification for the Signal conditioning needs to be 0 to -10v
and must draw no more than 1mA from the sensor and the op-amp supplies should supply no more than 30mW of power each.
here is the schematic of the circuit
first, we need to determine the value of R1
since the max input voltage is 1 and we want it be lower than 1mA
we can determine the value R1 =(1V)/1mA = 1kΩ
next, we need to determine the feedback resistor
since the max output voltage is 10
10V=Rf/1000
Rf=10KΩ
Next we need to determine Rx
since Rx is to be 1/4W resistor and we want to operate at half of its rated power
The worst case voltage across Rx occurs when Ry is set to zero
(1/8)W=(6^2)/Rx
Rx=1152Ω
Determine Ry
Assuming the value of Rx determined above and no loading on the divider
Ry that will yield 1V across it
1=[Ry/(288+Ry)]6
Ry=57.6Ω
The Thevenin equivalent of the divider circuit from the inverting amplifier
Rth=48Ω
and the thevenin resistance is at least a factor of 20 times smaller than the resistance value for Ri
Next, we devise the experiment
we record the values of the components
| Component | Nominal Value | Measured Value | Power or Current Rating |
| Ri | 1K Ω | 984Ω | 1/4W |
| Rf | 10k Ω | 9.9KΩ | 1/4W |
| Rx | 288 Ω | 287Ω | 1/4W |
| Ry | 57.6 Ω | 58.8Ω | 1/4W |
| V1 | 12V | 12.13V | 12W |
| V2 | 12V | 12.06V | 12W |
Next we build the circuit on the breadboard
Next we record the data from the output by looking at the multimeters we set up for the experiments
| Vin (V) | Vout(Measured)(V) | GAIN(Calculated) | V_Ri(mA) | I_Ri(Calculatd)(mA) | V_Rf(Measrued)(V) |
| 0 | -0.05 | 0 | -0.007 | -0.007113821 | 0.06 |
| 0.25 | -2.54 | -10.16 | 0.269 | 0.273373984 | 2.57 |
| 0.5 | -5.08 | -10.16 | 0.536 | 0.544715447 | 5.12 |
| 0.75 | -7.56 | -10.08 | 0.797 | 0.80995935 | 7.62 |
| 1 | -9.91 | -9.91 | 0.946 | 0.961382114 | 9.91 |
Power supply current
Iv1=2.32mA
Iv2=1.49mA
P_V1=12.13*2.32mA=28.14mW
P_V=12.06*1.49mA=17.97mW
Both power supply are less than 30 mW.
Subscribe to:
Posts (Atom)